class ix maths Chapter 8
CLASS IX







SUBJECT :- MATHS
CHAPTER :- QUADRILATERALS
Exercise 8.1
1. If the diagonals of a parallelogram are equal, then show that it is a rectangle.
यदि एक समांतर चतुर्भुज के विकर्ण बराबर हों, तो दर्शाइए कि वह एक आयत है।
2. Show that the diagonals of a square are equal and bisect each other at right angles.
दर्शाइए कि एक वर्ग के विकर्ण बराबर होते हैं और परस्पर समकोण पर समद्विभाजित करते हैं।
3. Diagonal AC of a parallelogram ABCD bisects ∠A (see Fig. 8.11). Show that:
(i) it bisects ∠C also,
(ii) ABCD is a rhombus.
समांतर चतुर्भुज ABCD का विकर्ण AC कोण A को समद्विभाजित करता है (देखिए आकृति 8.11)। दर्शाइए कि:
(i) यह ∠C को भी समद्विभाजित करता है।
(ii) ABCD एक समचतुर्भुज है।
4. ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that:
(i) ABCD is a square
(ii) Diagonal BD bisects ∠B as well as ∠D.
ABCD एक आयत है जिसमें विकर्ण AC दोनों कोणों A और C को समद्विभाजित करता है। दर्शाइए कि:
(i) ABCD एक वर्ग है
(ii) विकर्ण BD दोनों कोणों B और D को समद्विभाजित करता है।
5. In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see Fig. 8.12). Show that:
समांतर चतुर्भुज ABCD के विकर्ण BD पर दो बिंदु P और Q इस प्रकार स्थित हैं कि DP = BQ है (देखिए आकृति 8.12)। दर्शाइए कि:
(i) ∆APD ≅ ∆CQB
(ii) AP = CQ
(iii) ∆AQB ≅ ∆CPD
(iv) AQ = CP
(v) APCQ is a parallelogram
APCQ एक समांतर चतुर्भुज है।
6. ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (see Fig. 8.13). Show that:
ABCD एक समांतर चतुर्भुज है तथा AP और CQ शीर्षों A और C से विकर्ण BD पर क्रमशः लम्ब हैं (देखिए आकृति 8.13)। दर्शाइए कि:
(i) ∆APB ≅ ∆CQD
(ii) AP = CQ
7. ABCD is a trapezium in which AB || CD and AD = BC (see Fig. 8.14). Show that:
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ∆ABC ≅ ∆BAD
(iv) Diagonal AC = Diagonal BD
Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E.
7. ABCD एक समलंब है, जिसमें AB || DC और AD = BC है (देखिए आकृति 8.14)। दर्शाइए कि:
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ∆ABC ≅ ∆BAD
(iv) विकर्ण AC = विकर्ण BD
[संकेत: AB को बढ़ाइए और C से होकर DA के समांतर एक रेखा खींचिए जो AB को E पर प्रतिच्छेद करे।]
---
Exercise 8.2
1. ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively (see Fig. 8.29). AC is a diagonal. Show that:
(i) SR || AC and SR = ½ AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
ABCD एक चतुर्भुज है जिसमें P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिंदु हैं (देखिए आकृति 8.20)। AC उसका एक विकर्ण है। दर्शाइए कि:
(i) SR || AC और SR = ½ AC
(ii) PQ = SR
(iii) PQRS एक समांतर चतुर्भुज है।
2. ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
ABCD एक समचतुर्भुज है और P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिंदु हैं। दर्शाइए कि चतुर्भुज PQRS एक आयत है।
3. ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
ABCD एक आयत है, जिसमें P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिंदु हैं। दर्शाइए कि चतुर्भुज PQRS एक समचतुर्भुज है।
4. ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see Fig. 8.30). Show that F is the mid-point of BC.
ABCD एक समलंब है, जिसमें AB || DC है। साथ ही, BD एक विकर्ण है और E भुजा AD का मध्य-बिंदु है। E से होकर एक रेखा AB के समांतर खींची गई है, जो BC को F पर प्रतिच्छेद करती है (देखिए आकृति 8.21)। दर्शाइए कि F भुजा BC का मध्य-बिंदु है।
5. In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see Fig. 8.31). Show that the line segments AF and EC trisect the diagonal BD.
एक समांतर चतुर्भुज ABCD .में E और F क्रमशः भुजाओं AB और CD के मध्य-बिंदु हैं (देखिए आकृति 8.22)। दर्शाइए कि रेखाखंड AF और EC विकर्ण BD को समत्रिभाजित करते हैं।
6. Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
एक चतुर्भुज की विपरीत भुजाओं के मध्य-बिंदुओं को जोड़ने वाले रेखाखंड एक-दूसरे को समद्विभाजित करते हैं, इसे दर्शाइए।
7. ABC is a triangle right-angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that:
(i) D is the mid-point of AC
(ii) MD ⊥ AC
(iii) CM = MA = ½ AB
ABC एक त्रिभुज है जिसका कोण C समकोण है। कर्ण AB के मध्य-बिंदु M से होकर BC के समांतर खींची गई रेखा AC को D पर प्रतिच्छेद करती है। दर्शाइए कि:
(i) D भुजा AC का मध्य-बिंदु है।
(ii) MD ⊥ AC है।
(iii) CM = MA = ½ AB है।
---
---
📐 Theorem 8.1
English:
A diagonal of a parallelogram divides it into two congruent triangles.
Hindi (प्रमेय 8.1):
एक समांतर चतुर्भुज की एक विकर्ण उसे दो सर्वांगसम त्रिभुजों में विभाजित करती है।
---
📏 Theorem 8.2
English:
In a parallelogram, opposite sides are equal.
Hindi (प्रमेय 8.2):
एक समांतर चतुर्भुज में विपरीत भुजाएँ बराबर होती हैं।
---
🔺 Theorem 8.3
English:
If each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram.
Hindi (प्रमेय 8.3):
यदि किसी चतुर्भुज की प्रत्येक जोड़ी विपरीत भुजाएँ बराबर हों, तो वह समांतर चतुर्भुज होता है।
---
🔻 Theorem 8.4
English:
In a parallelogram, opposite angles are equal.
Hindi (प्रमेय 8.4):
एक समांतर चतुर्भुज में विपरीत कोण बराबर होते हैं।
---
🔷 Theorem 8.5
English:
If in a quadrilateral, each pair of opposite angles is equal, then it is a parallelogram.
Hindi (प्रमेय 8.5):
यदि किसी चतुर्भुज की प्रत्येक जोड़ी विपरीत कोण बराबर हों, तो वह समांतर चतुर्भुज होता है।
---
📐 Theorem 8.6
English:
The diagonals of a parallelogram bisect each other.
Hindi (प्रमेय 8.6):
एक समांतर चतुर्भुज की विकर्णें एक-दूसरे को समद्विभाजित करती हैं।
---
🔷 Theorem 8.7
English:
If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
Hindi (प्रमेय 8.7):
यदि किसी चतुर्भुज की विकर्णें एक-दूसरे को समद्विभाजित करती हों, तो वह समांतर चतुर्भुज होता है।
---
📏 Theorem 8.8
English:
The line segment joining the mid-points of two sides of a triangle is parallel to the third side.
Hindi (प्रमेय 8.8):
किसी त्रिभुज की दो भुजाओं के मध्य बिंदुओं को मिलाने वाली रेखाखंड तीसरी भुजा के समांतर होती है।
---
📏 Theorem 8.9
English:
The line drawn through the mid-point of one side of a triangle, parallel to another side, bisects the third side.
Hindi (प्रमेय 8.9):
किसी त्रिभुज की एक भुजा के मध्य बिंदु से खींची गई रेखा, यदि दूसरी भुजा के समांतर हो, तो वह तीसरी भुजा को समद्विभाजित करती है।




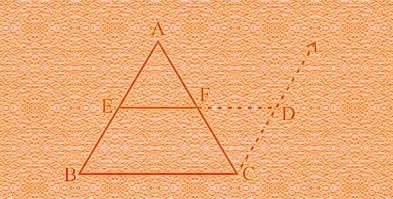

Comments
Post a Comment